top of page

Publications and Preprints

Chaotic heteroclinic networks as models of switching behavior in biological systems
We build chaotic heteroclinic networks that can reproduce stochastic switching dynamics observed in biological systems. Our heteroclinic network is fit to reproduce C. elegans behavioral sequences, producing the same dwell times and transition statistics.
Morrison, M., & Young, L. S. (2022). Chaotic heteroclinic networks as models of switching behavior in biological systems. Chaos: An Interdisciplinary Journal of Nonlinear Science, 32(12).
Transitions between peace and systemic war as bifurcations in a signed network dynamical system
We present a signed network model of cooperation and conflict dynamics in the context of international relations between states. Model simulations exhibit a sharp bifurcation from peace to systemic war as structural balance pressures increase, a bistable regime in which both peace and war stable equilibria exist, and a hysteretic reverse bifurcation from war to peace.
Morrison, M., Kutz, J. N., & Gabbay, M. (2022). Transitions between peace and systemic war as bifurcations in a signed network dynamical system. Network Science, 1-44.
Solving nonlinear ordinary differential equations using the invariant manifolds and Koopman eigenfunctions
We introduce a method for constructing eigenfunctions from a nonlinear ODE's invariant manifolds; this method allows us to find analytical solutions for certain types of nonlinear 2-dimensional ordinary differential equations that have real 1-dimensional invariant manifolds.
Morrison, M., & Kutz, J. N. (2022). Solving nonlinear ordinary differential equations using the invariant manifolds and Koopman eigenfunctions. arXiv preprint arXiv:2208.08529.

Nonlinear control of networked dynamical systems
We introduce a method for controlling the movement between fixed points in high-dimensional networked nonlinear systems using a feedforward control framework.
Our method integrates dimensionality reduction, bifurcation theory, and model discovery to find low-dimensional subspaces where feed-forward control can be used to manipulate a system to a desired outcome.
Morrison, M., & Kutz, J. N. (2020). Nonlinear control of networked dynamical systems. IEEE transactions on network science and engineering, 8(1), 174-189.

Nonlinear control in the nematode C. elegans
The neural activity of C. elegans associated with behavior is dominated by switching dynamics on a low-dimensional manifold. We propose a global, nonlinear control model which captures the state transitions described by Markov-switching models with a single dynamical system.
Morrison, M., Fieseler, C., & Kutz, J. N. (2021). Nonlinear control in the nematode C. elegans. Frontiers in Computational Neuroscience, 14, 616639.
Community detectability and structural balance dynamics in signed networks
We investigate the spectra of signed networks with community structure and find detectability transitions for community structure. Once community structure passes the detectability threshold it becomes the strongest network structure and dominates the entire network under structural balance dynamics.
Morrison, M., & Gabbay, M. (2020). Community detectability and structural balance dynamics in signed networks. Physical Review E, 102(1), 012304.
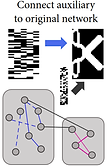
Preventing neurodegenerative memory loss in Hopfield neuronal networks using cerebral organoids or external microelectronics
In this computational study, we connect trained auxiliary networks to damaged Hopfield networks to aid in memory recovery. This study is an investigation into how brain-machine interfaces may be able to compensate for memory loss.
Morrison, M., Maia, P. D., & Kutz, J. N. (2017). Preventing neurodegenerative memory loss in Hopfield neuronal networks using cerebral organoids or external microelectronics. Computational and Mathematical Methods in Medicine, 2017.
bottom of page